The Rigveda And Baudhayana - Pythagoras Theorem
To claim that the Babylonians preceded the enunciation of the classic theorem by Pythagoras appears a trifle biased and ignorant.
Total Views | 745
DEDICATION:

Quoted in “History of Hindu Mathematics, A Source Book, Parts I and 2”, by Dutta , B. and Singh A.N., 1935, published by Asia Publishing House, Calcutta, copyright 1938.
It was with interest that I read a recent spurt of articles on Babylonian clay tablets in the lay press (readers may search on Google the following keywords: ‘Babylonian tablet’, ‘Pythagoras Theorem’, and see for themselves) which “established” that the Babylonians solved the Theorem more than 1000 years before the Greek philosopher was born.
The Tablets were originally discovered way back in 1937, and elaborate explanations and expositions have been written about them. It has been recently worked out why these tablets were created in the first place - apparently they played an important role in estimating land area for computation of land revenue.
To claim that the Babylonians preceded the enunciation of the classic theorem by Pythagoras appears a trifle biased and ignorant, considering that the development of Mathematics was in a much greater state of advancement in ancient Bharat FAR AHEAD of the Babylonians.
Of course, not surprisingly, such facts are often studiously ignored in the Western press for whatever reasons, and sadly, by their equally biased media devotees, in Bharat.
I have taken it upon myself therefore to enlighten my readers on the findings of learned mathematicians and historians as to the Vedic origins of the concepts behind the Theorem of Baudhayana ascribed to Pythagoras.
Vedic mathematicians knew all about the theorem MUCH before Babylonians
“…… long before 1943 people had pointed out that sacred books of the East contain "Pythagorean numbers". Such numbers are mentioned in the Sulvasutras, ancient Indian works on altar constructions of the triples, for example (8, 15, 17), satisfy the basic property for Pythagorean triples”
“………… the application (to ritual Vedic altar construction) involves geometric algebra, and there is no evidence of geometric algebra from Babylonia.
………… Hence we do not hesitate to place the Vedic altar rituals, or more exactly, rituals exactly like them , far back of 1700 B.C.” (Ref. 1). (Author’s note: Babylonian clay tablets are dated back to circa 1600 -1900 B.C.).
Dating the geometric knowledge of Ancient India
“ ……. the mathematical knowledge recorded in these (Sulba)sutras (aphorisms) are much more ancient; for the Sulba authors emphasise that they were merely stating facts already known to the composers of the Brahmanas and Samhitas of the early Vedic age ([3], [1], [2]).”
“The Sulbasutras give a compilation of the results in mathematics that had been used for the designing and constructions of the various elegant Vedic fire-altars right from the dawn of civilization…….. Constructions of the fire-altars are described in an enormously developed form in the Satapatha Brahmana (c. 2000 BC; vide [3]); some of them are mentioned in the earlier Taittiriya - Samhita (c. 3000 BC; vide [3]); but the sacrificial fire-altars are referred - without explicit construction - in the even earlier Rig Vedic Samhitas, the oldest strata of the extant Vedic literature.”
“An amazing feature of all ancient Indian mathematical literature, beginning with the Sulbasutras, is that they are composed entirely in verses - an incredible feat!
This tradition of composing terse sutras, which could be easily memorised, ensured that, inspite of the paucity and perishability of writing materials, some of the core knowledge got orally transmitted to successive generations.” (Ref. 2). (Author’s note: This accounts for the paucity of early written records pertinent to the Theorem).
The first recorded enunciation of the Theorem was by Baudhayana.
“The ´Sulba-sutra of Baudhayana (estimated 800 BCE or earlier) is the world’s oldest known mathematical text”.(Author’s note: see below for 3200 BCE estimate).
“The ´Sulba texts (composed several centuries before Pythagoras (c. 540 BCE) and Euclid (c.300 BCE)) show insights on the geometric and algebraic aspects of the properties of triangles, squares, rectangles, parallelograms, trapezia and circles. Plane geometry stands on two important pillars having applications throughout history: (i) the result popularly known as the “Pythagoras theorem” and (ii) the properties of similar figures. Both the features have a striking presence in the ´Sulba texts.
“ ………. the earliest explicit statement of the theorem occurs in the Baudhayana ´Sulba-sutra (1.48) in the following form:
(Translated from the Sanskrit, it reads,) “The diagonal of a rectangle produces [area] which its length and breadth produce separately.”
“Thus, Baudhayana states that the square on the diagonal of a rectangle is equal (in area) to the sum of the squares on the two sides.16”.
“From the references to fire-altars whose constructions require the knowledge of the Baudhayana-Pythagoras Theorem, both B. Datta ([7]) and A. Seidenberg ([26]) have concluded that the result was known at the time of the Vedic treatises ´Satapatha Braahmana and the still earlier Taittirıya Samhita. Again, as the doubling of a square is necessary for the construction of certain altars which are mentioned even in the Rigveda (oldest Veda), B. Datta concludes that at least the special case of the theorem (for the square) was known by the time of the Rigveda.” (Ref. 3).
Dating the Rigveda
“In 1985 ……………. the Indian National Science Academy (one of the most respected science academies in the world) published a volume, History of Astronomy in India wherein the Harappan civilization and the Brahmana period are correlated, and the Rig Veda is dated to about 7th millennium B.C.”, (Ref. 4).
“Astronomical references in Rigveda represent the sky views of important dates from 7000 BC to 5000 BC (9000 BP-7000 BP)….. The position of Ashvinis (in Aries) matched that of the Winter Solstice about 9000 years ago (7000 BC) as shown in the sky views”, (establishing that the Rigveda was composed around 7000 BCE).(Ref. 5).
VEDIC MATHEMATICS WAS THE MOTHER OF ALL MATHEMATICS
“‘I have concluded that not only are the Sulvasutras pre-Greek, but that even the Old-Babylonian mathematics derives from a system of practices much like those disclosed in the Indian sacred works.’….. Seidenberg’s conclusion that Vedic mathematics is older than that of 1700 BC Babylon is confirmed now since it is clear14 that the Agnicayana altar, whose mathematics he considered, leads to 3000 BC on astronomical grounds.”(Ref. 6).
“A closer, unbiased study of Vedic mathematics has shown that the commonly held view of Mesopotamia being the cradle of civilisation may not be true………. “The common source, as per Seidenberg, was Vedic Mathematics — the mother of all ancient mathematics. ………….. Seidenberg’s assessment seems to be true: That the sciences, including mathematics, were nurtured in India long before Mesopotamia and Egypt.
The two civilisations, in fact, borrowed from India. Navaratna Rajaram and David Frawley write in their book, ‘Vedic Aryans and the Origins of Civilisation’, “The evidence of the Sulbas, notably the fact that Old-Babylonia and Egypt both derive their mathematics from them, places the early Sutra literature firmly before 2000 BCE, the date of the Egyptian Middle Kingdom.”
“Interestingly, astronomical references in the work of Asvalayana push this date for the Sulbasutras even further— to around 3100-2600 BCE.”, (Ref. 7).
“The origins of geometry have been very clearly traced to thousands of years BC. It has been proven that one of the Vedic experts Baudhyayana, lived around 3200 BCE.”
“It was the Shulba Sutras that recorded the basis of these geometric formulas used for the Vedic temples and altars. …… how to make a square of the same area as that of a triangle …..”
“…….. India was indeed the centre for most civilizational development of the time. One example is that recent evidence of geometrical drawing instruments from as early as 2500 BCE have been found in the Indus Valley. Weights and scales with decimal divisions have been found from that early period, all of which are still quite accurate.”
“In 1978, Dr. Abraham Seidenberg, a professor of mathematics at the University of California in Berkeley, as noted in a paper called The Origin of Mathematics (p. 301, 1978), mentioned….. Old Babylonia (1700 BC) got the theorem of Pythagoras from India….”
“ ……. in this paper, Seidenberg established that the Shulba Sutras were the basis for the mathematics in Egypt, Babylon, and Greece…… preceded the mathematics of both Old Babylonia (c. 1900-1750 BCE) and of the Egyptian Middle Kingdom (c. 2100-1800 BCE).” (Ref. 8).
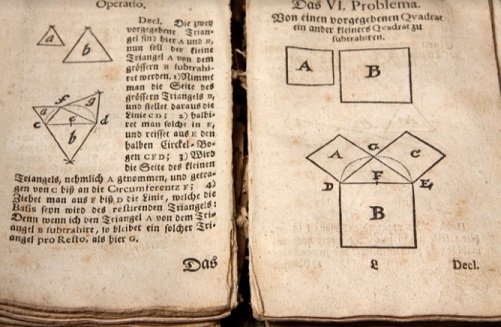
Reproduction from mathematics textbook dated 1743; iStock image, licensed to author, U.K.Sharma
Did Babylonian clay tablets describe the Pythagoras Theorem at all?
“The artifact, named Si.427,(Babylonian clay tablet) …………. dates from the Old Babylonian (OB) period – 1900 to 1600 BCE,” said Mansfeld. “It’s the only known example of a cadastral document from the OB period, which is a plan used by surveyors define land boundaries
(https://link.springer.com/article/10.1007/s10699-021-09806-0). In this case, it tells us legal and geometric details about a field that’s split after some of it was sold off".” (Ref. 9).
“Pythagoras theorem was known in other ancient civilizations like the Babylonian, but the emphasis there was on the numerical and not so much on the proper geometric aspect while in the Sulbasutras one sees depth in both aspects - especially the geometric. This is a subtle point analysed in detail by Seidenberg.”
‘“ ……….. the basic point is that the dominant aspect of Old Babylonian mathematics is its computational character ... The Sulvasutras know both aspects (geometric and computational) and so does the Satapatha Brahmana." A Seidenberg’, (Ref. 2).
Did Pythagoras visit Bharat?
“…what became known as the Pythagorean theorem was already existing in the Baudhyayana, the earliest of the Shulba Sutras. This was presented by Pythagorus around 540 BCE after he discovered it in, what some say, his travels to India.” (Ref. 8).
Pythagoras lived in sixth century BCE Greece; and the third century CE sophist Philostratus says that Pythagoras studied under Hindu sages in India, (Refs.10, 11 and 12).
Concluding remarks
The gifts that Bharat gave to the world are innumerable and unimaginable. Bharat’s contributions in mathematics alone, which in turn have impacted every aspect of our daily life, albeit unbeknown to us all. The impact has been felt silently through research, engineering, space exploration, architecture, everywhere.
Historians of mathematics have elegantly demonstrated that the geometric concepts inherent in the enunciation of the Pythagoras Theorem were well known to Ancient Indian Mathematicians, and were in fact derived from Vedic understanding of geometry. The RigVeda where the earliest mention is found, was composed around 7000 BC, thus establishing that “Pythagorean” principles were familiar to Vedic Sages of Bharat. The Mesopotamian, Egyptian and Babylonian civilisations learned mathematics laid down by Vedic mathematicians of Ancient India. The EARLIEST WRITTEN exposition of the Pythagoras Theorem itself was by Baudhayana in 800 BC or earlier, pre-dating the enunciation by Pythagoras himself. Babylonian concepts were merely used for computation, and did not elaborate on geometric principles as per reputed mathematical historians.
Find the references here;
--
Bharati Web








